Les trackers : petite analyse mathématique

Les trackers, ou ETF pour Exchange Traded Funds ((Il semble qu’il y ait une subtile différence entre ETF et trackers, mais elle ne change rien au fond ce cet article.)) : que sont-ils, pourquoi leur valeur s’érode-t-elle avec le temps, serait-il possible de faire des trackers conservatifs (qui ne s’érodent pas) ?

Quand j’entends sur BFM, François Monnier, du journal Investir, conseiller aux particuliers l’usage du tracker BX4, pourquoi cela me fait-il bondir ?

Présentation des trackers

« Un tracker est un fonds qui réplique la performance d’un indice et qui est coté en bourse. Il permet à l’investisseur de détenir l’équivalent de l’indice en question sans avoir besoin d’acheter toutes les actions qui composent cet indice. » (Vernimmen). Précisons cela.

Soit un indice sous-jacent, de valeur (action, indice ou tout autre produit), qui varie de pendant un certain laps de temps. Un tracker est un titre de valeur qu’on peut acheter comme une action et dont les variations suivent celles du sous-jacent, avec éventuellement un effet de levier .

Tout le coeur de la problématique que nous allons discuter vient du fait que le suivi entre l’ETF et son sous-jacent se fait de façon relative et finie : quand le sous-jacent varie de / %, l’ETF augmente proportionnellement, de / %. Cela s’écrit mathématiquement :

Il y a des trackers simples, ceux pour lesquels = 1 : une augmentation de 1 % du sous-jacent implique une augmentation de 1 % du tracker.

Il y a aussi des trackers à effet de levier : > 1, par exemple = 2, voire plus. Il y a aussi des trackers inverses : = -1, dits trackers bear ou short, à l’inverse des précédents dits bull ou long ; une augmentation de 1 % du sous-jacent implique alors une diminution de 1 % du tracker.  Exemple : le Lyxor ETF Short CAC 40. Les trackers inverses peuvent être à effet de levier : < -1.

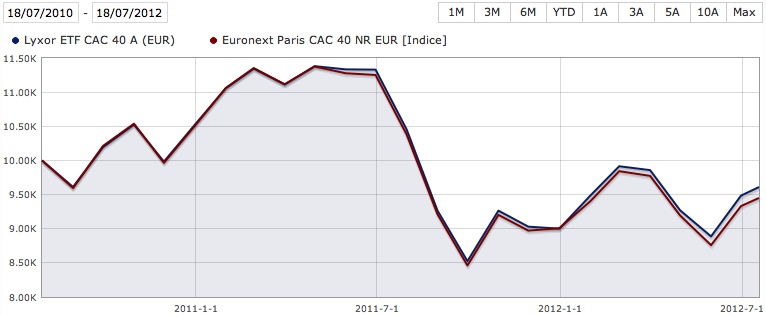
Dans la figure ci-dessous un exemple de tracker simple, le Lyxor ETF CAC 40, en bleu, comparé au CAC 40, en rouge, sur deux ans : le tracker suit bien le sous-jacent ((À de toutes petites différences près, négligeables pour notre propos. Ici, j’ai représenté le CAC 40 NR (net return) parce que la référence de l’ETF, le CAC 40 GR (global return), n’était pas accessible sur le site utilisé (Morning Star).)).

Par contre, de façon générale, les trackers à effet de levier ne suivent pas le sous-jacent, c’est ce que nous allons voir maintenant.

Problématique : érosion, dit effet beta-slippage

Les trackers suivent en instantanée leur sous-jacent mais ne reproduisent pas exactement les variations de long terme du sous-jacent (sauf éventuellement pour = 1) : si à long terme le sous-jacent augmente de %, le tracker n’augmente pas de %. Cette effet est appelé le beta-splippage, ou –slippage, en anglais, parce que cette érosion augmente avec la volatilité ((Le beta indique la volatilité d’un titre ou d’un portefeuille de titres par rapport au marché. « Par exemple, si le beta d’une action est de 0,8, son cours a varié en moyenne dans la periode précédente de 0,8 % quand le marché variait de 1 %. Autrement dit c’est la sensibilité ou élasticité du cours du titre par rapport à l’indice boursier représentant le marché » (Wikipedia). Suivant certaines théories financières, le bêta historique mesure le risque systématique sur une longue période mais cette affirmation ne fait aucun sens pour les investisseurs value.)). On pourrait dire, en langage un peu scientifique, que les trackers à effet de levier sont non conservatifs, mais vous allez voir que ça n’a rien de sorcier.

Explication

On sait qu’une augmentation de 10 % puis une diminution de 10 % ne fait pas une variation nulle mais une diminution de 1 % car : 100 + 10 % = 110 puis 110-10 % = 99. Autrement dit, l’inverse d’une augmentation de 10 % n’est pas une diminution de 10 % : une augmentation de 10 % est une multiplication par 1,1, l’inverse de cette augmentation est une division par 1,1 et pas une multiplication par 0,9. Tout le problème est là, dans cette évidence que chacun connaît.

Comment cela s’applique-t-il aux trackers ? Facile : une augmentation de 20 % puis une diminution de 10 % fait : 100 + 20 % = 120 puis 120 – 10 % = 108 ; or une diminution de 20 % puis une augmentation de 10 % fait : 100 – 20 % = 80 puis 80 + 10 % = 88. Dans le premier cas, on a finalement une augmentation de 8 % et dans le deuxième cas, une diminution de 12 % alors que les opérations semblent opposées. Ceci montre qu’un tracker inverse ne reproduit pas les variations long-terme du sous-jacent : j’appelle ça un tracker non conservatif ((Par contre une diminution puis une augmentation de 10 % donne la même chose qu’une augmentation puis une diminution : 100 – 10 % = 90 puis 90 + 10 % = 99. C’est un ‘hasard’ qui n’arrive jamais en pratique : la baisse est rarement strictement égale à la hausse qui précède.)). Fait accablant : dès qu’il y a une certaine volatilité le tracker à effet de levier finit toujours par perdre par rapport au sous-jacent ((A faible volatilité, un tracker à effet de levier peut gagner par rapport au sous-jacent. On pourra s’en rendre compte en considérant deux augmentations successives de 10 % et un effet de levier 2. Néanmoins, si on attend suffisamment longtemps, on franchit toujours un seuil à partir duquel le tracker est défavorable. Je ne précise pas le seuil en question, il dépend  de la volatilité et du temps. Et plus on attend longtemps plus l’érosion augmente.)). En effet le raisonnement précédent est valable quel que soit le sens de variation : 88 représente une perte de 12 au lieu de 8, 108 représente un gain de seulement 8 au lieu de 12 !

Idem pour les trackers à effet de levier. Pour un levier de 2 alors : 100 + 40 % = 140 puis 140 – 20 % = 112. Cela fait 12 % d’augmentation alors que le sous-jacent a augmenté de 8 %.

Autre démonstration qui me semble encore plus parlante. Imaginons que le sous-jacent augmente de 10 % puis revienne à son point de départ :

100 + 10 % = 110 puis 110 – 9,0909 % = 100.

100 + 20 % = 120 puis 120 – 18,1818 % = 98,1818.

En fait, seuls les trackers simples (=1) sont conservatifs.

Ordre de grandeur de l’effet

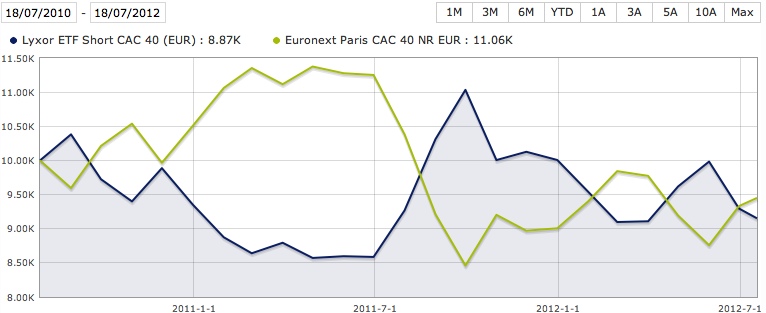
Dans la figure ci-dessous, un exemple de tracker inverse, le Lyxor ETF Short CAC 40, en bleu, comparé au CAC 40, en jaune, sur deux ans : le tracker suit l’opposé du sous-jacent mais s’érode avec le temps. Après deux ans, le CAC a perdu 5 %, et au lieu d’avoir gagné 5 %, le tracker inverse a perdu 9 % !

L’effet beta-slippage n’est pas donc négligeable du tout.

Vous allez peut-être penser que cet effet est inhérent à l’effet de levier. Et bien non ! On pourrait très bien réaliser des trackers conservatifs. Je vais vous le prouver.

Les trackers pourraient être conservatifs

Les trackers ne sont pas conservatifs parce que l’équation (1) n’est utilisée (en mathématiques on dirait résolue) que sur des variations petites mais non infinitésimales. Pour solutionner le problème, il suffirait de considérer des pas infinitésimaux c’est-à-dire de résoudre l’équation de façon théorique. Pour un élève d’une terminale scientifique, c’est facile, la solution de l’équation (1) est donnée par :

avec une constante. Prenons, par exemple, un tracker à effet de levier double, qui vaut 1 quand le sous jacent vaut 1; cela donne

Si le sous-jacent augmente de 10 % alors = 1,1 x 1,1 = 1,21. Certes ce n’est pas 1 + 20 % mais, comme chacun le sait, deux fois une augmentation de 10 % ne fait pas une augmentation de 20 % mais de 21 % (( Pour un inverse on trouve z=1/x. Si le sous-jacent augmente de 8 % alors z = 1/1,08 = 0,9259. )).

La relation (2) est donc parfaitement conservative : il n’y a pas d’érosion.  Mais les fournisseurs d’ETF n’ont probablement aucun intérêt à appliquer une telle relation. Mieux : si jamais un tel ETF inverse voit le jour, je vous promets de l’acheter… je ne risque pas grand-chose…

Simulation numérique

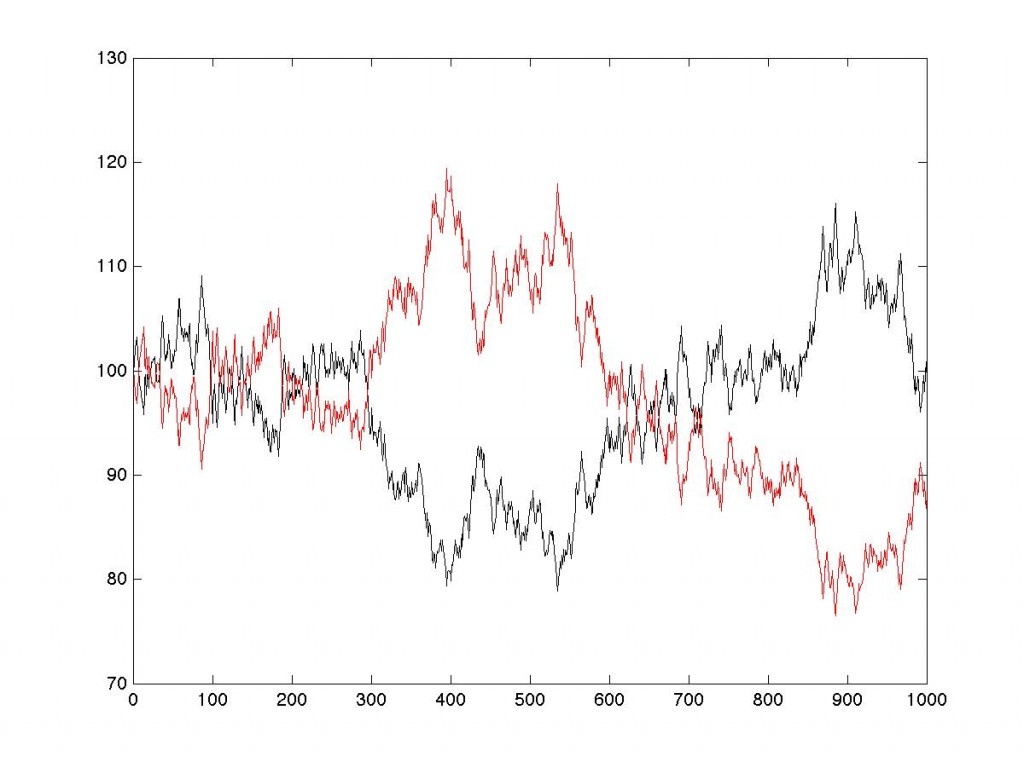
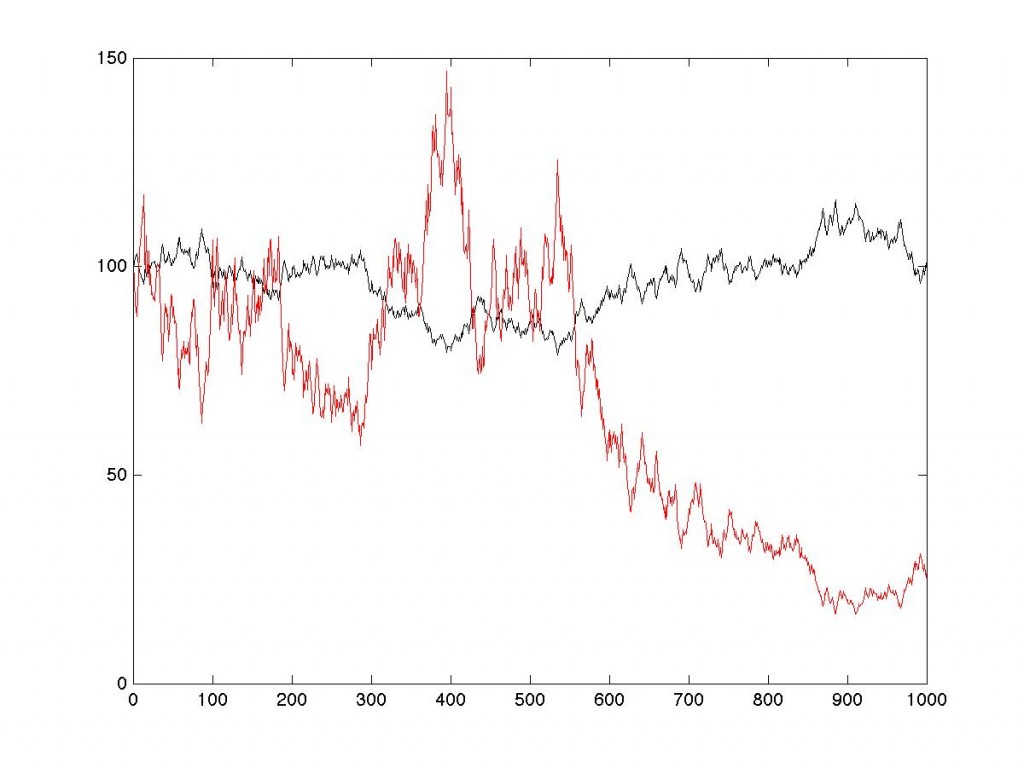
Pour vous convaincre complètement, j’ai réalisé une expérience numérique : j’ai simulé un cours de bourse fictif en tirant aléatoirement 1000 nombres compris entre -2 % et +2 %. Puis, partant d’un cours de 100, j’ai ajouté ces variations. Afin de rendre la simulation plus parlante, je me suis juste arrangé pour qu’après 1000 simulations, le cours revienne à 100 (pas de tricherie là dedans, il suffit de faire une série de tirages aléatoires de moyenne nulle). Voici en noir le résultat, c’est-à-dire le sous-jacent, et en rouge ce que donne la relation (1) avec   = -1, c’est-à-dire un tracker inverse. Après 1000 variations, l’indice est revenu à 100 alors que le tracker a perdu plus de 10 %. C’est purement mathématique vous dis-je.

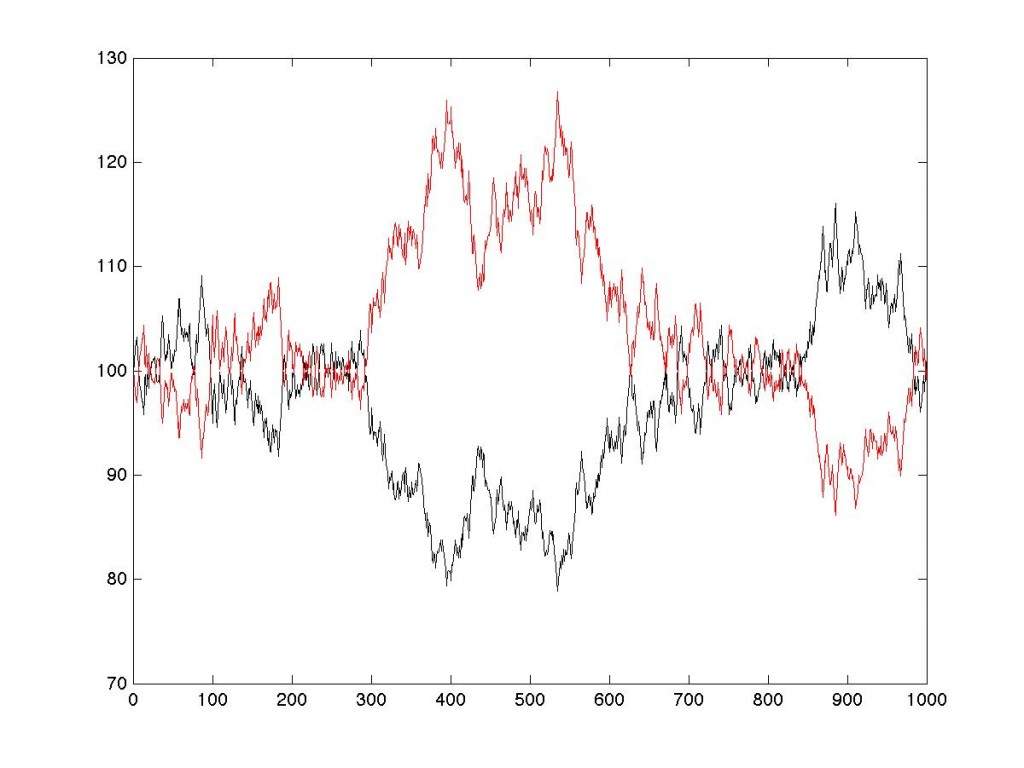
Évidemment, avec un tracker qui serait conservatif, c’est-à-dire avec ma relation (2), on reviendrait parfaitement à 100 :

Plus le levier est grand, plus l’effet d’érosion est grand. Voici ce que donnerait un levier de -4, l’ETF perd 75 % de sa valeur…

Conclusion

Si, par exemple, vous achetez un tracker à effet de levier lorsque le sous-jacent vaut 100, que vous le gardez longtemps, puis que le sous-jacent revient à la valeur 100, alors le tracker aura, lui, perdu de la valeur. C’est ce qu’on appelle l’érosion ou l’effet beta-slippage. Ces produits financiers ne doivent donc pas être conservés longtemps (disons pas plus de quelques mois). Seul le tracker sans effet de levier ( = 1) ne subit pas ce phénomène.

Les émetteurs de trackers pourraient éliminer cet effet mais n’oublions pas l’essentiel : ces outils sont faits pour faire gagner de l’argent… à leurs émetteurs, les établissements financiers.

Les trackers ont, en plus, des frais de fonctionnement annuels prélevés au fil de l’eau par l’émetteur. Ceux-ci sont variables selon les émetteurs et selon la nature de l’indexation, s’élevant de 0,10 % à 0,65 % (p.ex. 0,25 % par an pour le Lyxor ETF CAC 40). Ces frais sont finalement assez faibles au regard de l’érosion.

Pour moi, un ETF n’est pas un achat très value (sauf s’il l’on sait valoriser un panier de produits…). Mais, pour ceux qui voudraient tout de même contracter ce genre de produit, j’espère avoir pointé leurs (gros) inconvénients.

JL – 13 avril 2015.

$