Calculer la performance de son portefeuille

On pourrait penser que calculer la performance (que nous appellerons aussi rendement) d’un portefeuille est chose évidente. Pas tant que cela : il y a des méthodes aberrantes et plusieurs méthodes pertinentes.

I. Cas simple, sans apport intermédiaire.

Le seul cas simple est celui où il n’y a qu’un seul apport au portefeuille, l’apport initial. Alors, la performance est la différence relative entre le capital final et initial :

$r = (C_f - F_0) / F_0$

où :

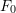$F_0$ = apport initial au temps 0,
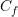$C_f$ = capital final au temps $T$ ,
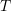$r$ = performance.

Cette performance est la performance période, c’est-à-dire la performance sur l’ensemble de la période $T$ . Pour le ramener à une performance annuelle $R_1$ , c’est-à-dire sur un temps $T_1 =$ 1 an, il faut l’annualiser, ce qui par définition revient à utiliser la relation fondamentale

$(1+R_1)^{1/T_1} = (1+r)^{1/T} \quad (a)$

ce qui donne pour calculer $R_1$ :

$R_1 = (1+r)^{T_1/T} - 1$

Un rendement est associé à une durée, et on passe d’une durée à une autre par la relation (a). A partir de maintenant, la performance ou le rendement sans autre précision désigneront la performance période.

Notons une autre relation fondamentale. Une somme initiale $F_0$ placée à ce rendement devient après un temps t la somme :

$F_t = F_0 \, (1+r)^{t/T} = F_0 \, (1+R_1)^{t/T_1}$

Exemple. Au 1er juillet 2012, mon portefeuille a une valeur de 5 000 €, au 1er mai 2013 il a une valeur de 5 738 €. Sa performance période est donc $r = (5 738 - 5 000) / 5 000 = 14,76 %$ . Sa performance annualisée est $R_1 = (1+0,1476)^{12 {\rm ~mois} /10 {\rm ~mois}} - 1 = 17,96 %$ . Si la performance continue à ce rythme, au 31 décembre 2013 mon portefeuille vaudra $5 000 \, (1+0,1476)^{18 {\rm ~mois} /10 {\rm ~mois}} = 6 406 €$ .

II. Quand tout se complique

Avec des apports (ou des retraits) intermédiaires, tout devient plus complexe. Il y a même des méthodes aberrantes. C’est le cas de la première qui vienne à l’esprit, en définissant encore la performance comme la différence entre le capital final moins le capital initial, divisé par le capital initial. Imaginons par exemple la situation suivante :

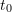$t_0$ : je mets 100 € dans le portefeuille.
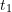$t_1$ : la valorisation n’a pas changé. Je rajoute 100 €.
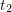$t_2$ : la valorisation n’a toujours pas changé.

Avec la définition proposée, on trouve que la performance est (200 – 100) / 100 soit 100%, absurde puisque je n’ai pas gagné d’argent.

Moins absurde semblerait être de faire la différence entre le capital final moins le capital total apporté, divisé par le capital total apporté. Dans l’exemple précédent, on trouverait une performance de (200 – 200) / 200 = 0 %, comme il se doit. Mais dans la situation suivante :

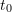$t_0$ : je mets 100 € dans le portefeuille
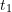$t_1$ : la valorisation monte de 10 %. Je retire 99 €. Le portefeuille vaut 11 €.
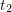$t_2$ : la valorisation n’a pas changé.

Avec la définition proposée, on trouve que la performance est (11-1)/1 = 1 000 % ce qui n’est pas beaucoup plus raisonnable que la solution précédente. Cela donne des solutions absurdes car nous n’avons pas fait intervenir le temps dans les calculs, c’est-a-dire le fait que les capitaux apportés ne travaillent pas sur la même durée.

III. Calcul avec des apports intermédiaires

Dans le cas général, il y a essentiellement deux façons de calculer une performance : la performance de la part, et la performance globale du portefeuille. Nous nous proposons de définir ces deux approches, et d’examiner comment on les calcule.

A. Deux ratios de performance

1. La performance de la part. En français, cela s’appelle aussi le Taux de Rentabilité Pondéré par le Temps (TRPT). En anglais, Time Weighted Rate of Return (TWRR). Le TRPT comptabilise :

La performance d’une sélection d’actions.
Le gain fait par des prises de plus-values à cours élevé, puis rachat à cours bas, mais ne prend pas en compte l’apport de performance permis par des entrées d’argent sur le portefeuille lorsque les cours sont bas. C’est la performance dont la publication est rendue obligatoire pour les gérants d’OPCVM, car on ne souhaite pas juger la performance d’un gérant sur le moment où les épargnants choisissent de souscrire ou racheter leurs parts d’OPCVM. C’est aussi la méthode requise quand entrent ou sortent des membres dans un club d’investissement.

2. La performance globale du portefeuille. En français, cela s’appelle aussi le Taux de Retour Interne (TRI), le taux actuarial, le taux effectif de rendement, le taux de rendement actuarial, etc. En anglaisMoney Weighted Rate of Return (MWRR) ou Internal Rate of Return (IRR). Ce taux comptabilise les apports au portefeuille et mesure donc la performance du gérant qui maîtrise les flux de capitaux. Cela peut être le cas de certains investisseurs particuliers.

Exemple. Imaginons le résultat suivant sur une période donnée

Rendement de la part : +12 %
TRI : +10 %
Indice de référence : +11 %.

Cela signifie que :

Part > indice : les valeurs choisies ont mieux performé que l’indice de référence.
TRI < indice : les apports ont été faits aux mauvais moments, c’est-à-dire sur valeurs de part élevées.

Il est en effet clair que si vous apportez du capital lorsque la part a une faible valorisation, vous gagnerez plus qu’en apportant ce capital sur une part mieux valorisée.

B. Définitions mathématiques

Les ratios reposent tous les deux sur le découpage du temps en $n$ périodes séparées par les apports ou les retraits du portefeuille.

Notations : Au temps $t_0=0$ , le capital initial $C_0$ est nul, on fait un apport en capital (flux) $F_0$ . Du fait des bénéfices ou pertes, au temps $t_1$ le capital est devenu $C_1$ , différent de $C_0$ . De façon générale, au temps $t_i \; (i=1,2,...,n-1)$ , le capital est devenu $C_i$ , on apporte alors $F_i$ (si $F_i<0$ il s’agit d’un retrait). Immédiatement après le temps $t_i$ , le capital est donc $C_i+F_i$ . Au temps final $T=t_n$ , le capital final est $C_f$ .

1. Définition de la performance de la part. Sur la période $t_{i-1}$ à $t_i$ , la valeur est passée de $C_{i-1}+F_{i-1}$ à $C_i$ . Le rendement sur cette période est donc

$r_i = C_i / ( C_{i-1}+F_{i-1} ) -1$

Le TRPT est défini comme le rendement composé :

$TRPT = (1+r_1)(1+r_2)(1+r_3)...(1+r_n) - 1. \quad (1)$

2. Définition du TRI (performance du portefeuille). L’apport $F_i$ travaille pendant un temps $(T-t_i)$ , s’il travaille avec un rendement $r$ , il devient au temps $T$ la somme $F_i (1+r)^{(T-t_i)/T}$ . Si tous les apports travaillent avec ce taux, alors au temps $T$ on doit avoir le capital (le symbole $\sum$ représente la somme):

$C_f = \sum_{i=0}^{n}\, F_i \, (1+r)^{(T-t_i)/T}.\quad (2)$

Le TRI est défini comme un nombre $r$ solution de cette équation. Il est aussi souvent présenté (c’est équivalent) comme la solution $r$ de l’équation :

$\sum_{i=0}^{n}\, F_i / (1+r)^{t_i/T} - C_f / (1+r) = 0. \quad(3)$

C’est donc le rendement défini par le fait que si tous les apports travaillent avec ce même rendement alors on obtient le capital final.

C. Calcul pratique.

1. TRPT. Le procédé le plus courant pour calculer le TRPT est de raisonner en parts :

Au départ, on divise le portefeuille en un nombre arbitraire de parts, souvent choisi de telle sorte que la valeur initiale de la part soit 1 ou 100.
Tant qu’il n’y a pas d’apport ou de retrait dans le portefeuille, la valeur de la part est donnée par la valeur du portefeuille (qui, elle, fluctue) divisé par le nombre de parts,
Lors d’un apport ou de retrait, on augmente ou diminue le nombre de parts de telle sorte que la valeur de la part reste constante. Exemple : j’ai 10 parts a 100 € soit 1000 € dans mon portefeuille, et j’apporte 250 € (donc = 2,5 parts). Après apport, le portefeuille compte donc 12,5 part a 100 € soit 1250 euros.
Ensuite, la valeur de la part recommence à fluctuer en fonction du marché.
La performance du portefeuille en % est la valeur de la part divisée par la valeur initiale de la part, moins un.

[Edition, novembre 2020.] On peut résumer cette façon de faire, qui correspond bien sûr à la relation (1), de façon simple :

Valeur de part au temps $t_i$ = Valeur de part au temps $t_{i-1}$ $\, \times$
Capital au temps $t_i$ avant apport / Capital au temps $t_{i-1}$ après apport.

2.TRI. Le calcul du TRI est plus complexe parce que la relation (3) possède plusieurs solutions et qu’elle ne peut être résolue que par approximations successives. Heureusement, elle est préprogrammée dans OpenOffice Classeur (ou Excel) sous la dénomination TRI.PAIEMENTS (la fonction de base TRI ne fonctionne que pour des apports à intervalles constants) avec la syntaxe

TRI.PAIEMENTS( $F_0:F_n;t_0:t_n;estimation$ )

où estimation (paramètre facultatif) est une estimation a priori du TRI dont la valeur par défaut est 10%. Attention, cette fonction de Excel lit des dates ou des nombres de jours mais donne une performance annualisée. Pour la remettre sur une période T, il faut faire $TRI(T) = (1+TRI) ^ {T/365 jours}-1 )$ (où $T$ est exprimé en jours).

3. Approximation de TRI ou Taux de Rentabilité Pondéré par le Capital (TRPC) ou Taux de Retour Pondéré par les Capitaux Investis (TRPCI). En anglais, j’ai l’impression que cela s’appelle Total Return Rate (TRR). Si on suppose que le TRI est petit, et que les flux initiaux ne sont pas trop grands devant les flux finaux, alors en développant la relation (2) linéairement, on trouve que le TRI est proche de

$TRPC = \left(C_f -\sum_{i=0}^{n}\, F_i \right) /\left( \sum_{i=0}^{n}\, (T-t_i)\,Fi / T \right). \quad (4)$

Au numérateur on reconnaît le bénéfice net : c’est la somme réellement gagnée ou perdue, au dénominateur ce que l’on appelle capital employé. Ce dernier est la somme des apports de capitaux, chacun étant pondéré par le temps passé à travailler. Cette valeur peut être utilisée pour la variable estimation de la fonction TRI.PAIEMENTS.

IV. Exemples

Exemple 1. Considérons le cas suivant :

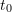$t_0$ : je mets 100 € dans le portefeuille. La part est a 100 €.
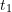$t_1$ : la valeur du portefeuille est montée de 10 % à 110 €. Je rajoute du capital pour une part soit 110 €.
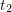$t_2$ : la valeur du portefeuille redescend de 9,09 % pour arriver à 200 €.

Il y a toujours 2 parts dont la valeur est de 100 €, la performance de la part est nulle. J’ai injecté 210 € et ai maintenant 200 €, j’ai donc perdu 10 €. Le TRI est donc négatif. Pour le calculer il faut avoir les valeurs des $t_i$ ; en prenant t0 = 0, $t_1$ = 365, $t_2$ = 730 je trouve TRI(excel) = -3,26 % par an soit TRI $= (1-0,0326)^2-1 = -6,41 %$ sur les deux ans.

Exemple 2. A l’inverse, en apportant du capital à un point bas de la part :

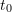$t_0$ : je mets 100 € dans le portefeuille. La part est a 100 €.
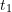$t_1$ : la valeur du portefeuille a baissé de 10 % soit 90 €. Je rajoute du capital pour une part, soit 90 €.
$_2$ : la valeur du portefeuille remonte de 11,11 % pour arriver à 200 €.

La performance de la part est nulle et j’ai gagné 10 €. En prenant $t_0 = 0$ , $t_1 = 365$ , $t_2 = 730$ je trouve TRI(excel) = +3,41 % par an soit TRI = +6,93 % sur les deux ans.

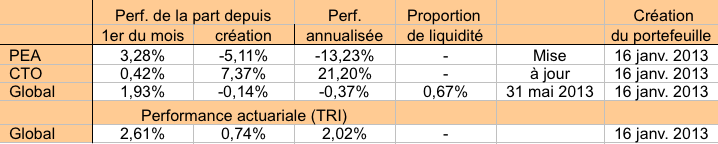
Exemple 3. Le tableau suivant montre un cas réel. On voit notamment que la performance de la part peut être négative (-0,14%) alors que l’on a gagné de l’argent (TRI = 0,74% > 0) : c’est parce que l’on a investi plus d’argent quand la part était basse que lorsqu’elle était haute.

Références

http://gestion.coursgratuits.net/economie/retours-et-taux-d-investissements.php
http://en.wikipedia.org/wiki/Internal_rate_of_return
https://fr.wikipedia.org/wiki/Taux_de_rentabilité_interne
http://en.wikipedia.org/wiki/True_Time-Weighted_Rate_of_Return
Une discussion sur le sujet : http://www.devenir-rentier.fr/viewtopic.php?pid=63058#p63058, notamment les posts de Chroom et Julien.
TWR : http://moneystore.be/2012/gestion/calculer-performance-dun-portefeuille
TRPC : http://jybaudot.fr/Banque/rentpond.html
Notice de la fonction TRI : http://office.microsoft.com/fr-fr/excel-help/tri-paiements-HP005209341.aspx
Considérations générales et très particulières, voir notamment p. 227 : http://www.actuaries.org/AFIR/Colloquia/Paris/Lam.pdf
Un document extrêmement complet et didactique sur le sujet : https://www.chsoft.ch/fr /assets/Dateien/files/PDF/ePoca/fr/Calcul de Performance en Pratique.pdf
Livres de mathématiques financières.

JL – juin 2013.

10 Responses to Calculer la performance de son portefeuille

Benjamin 5 novembre 2015 at 16 h 04 min

Bonjour,

Dans votre reporting mensuel, quelle formule appliquez-vous pour calculer la performance annualisée ?

Autre question : quel intérêt trouvez-vous à garder le CTO BINCK en plus du CTO IB ? Est-ce que seul le CTO IB ne suffirait-il pas ?

Merci d’avance pour vos réponses.

Cordialement,

Benjamin

Reply ↓
- Jerome Leivrek Post author 5 novembre 2015 at 18 h 10 min
  
  Bonjour Benjamin,
  
  Soit p la performance de la part depuis l’origine, je commence par calculer le nombre d’années (en nombre décimal) depuis l’origine en faisant n = nombre de jours depuis l’origine divisé par 365, puis la performance annualisée est = (1+p)^(1/n) – 1 (le ^ désigne une puissance).
  
  Il y a deux avantages à garder un CTO Binck : 1. déclarer ses revenus d’un compte IB est compliqué, moins on a de lignes dessus, mieux on se porte (surtout s’il y a des dividendes), 2. Binck donne accès à quelques marchés auxquels on n’a pas accès avec IB (notamment certaines valeurs sur la marché AIM de Londres).
  
  Bonne soirée,
  
  JL
  
  Reply ↓
srem 16 octobre 2018 at 9 h 54 min

Bonjour, je viens de trouver votre article.
Felicitations, je le trouve très bien fait et vraiment interessante.

Reply ↓
- Jerome Leivrek Post author 16 octobre 2018 at 9 h 58 min
  
  Merci Srem !
  
  Reply ↓
tonnick 25 janvier 2019 at 15 h 32 min

Bonjour,
d’après ma compréhension, la méthode des parts nécessite de connaître la valeur du portefeuille au moment de l’apport ou du retrait de capitaux, valeur dont je n’arrive pas à trouver l’historique sur Binck. Comment faîtes-vous? Notez-vous la valeur du portefeuille dès que vous effectuez un virement entrant ou sortant?
Merci d’avance et bravo pour votre site
Bonne journée

Reply ↓
- Jerome Leivrek Post author 27 janvier 2019 at 21 h 07 min
  
  Bonjour,
  Oui, quand je fais un virement sur mon portefeuille, je note la valeur de celui-ci.
  Si vous avez oublié de le faire, c’est récupérable, il suffit de rentrer la valeur à l’instant t mais en tenant compte intelligemment de ce qu’est de devenu votre somme virée entre-temps (je vous laisse réfléchir)…
  
  Reply ↓
  - tonnick 28 janvier 2019 at 16 h 05 min
    
    Bonjour,
    OK, merci pour votre retour. Je note la valeur de mon portefeuille quand je fais un virement, mais pas de façon systématique ; je dois pouvoir retrouver les valeurs manquantes en regardant l’évolution des cours des actions détenues, ce n’est effectivement pas infaisable, mais ça s’annonce fastidieux quand on a de nombreuses lignes en portefeuille…
    Au plaisir de vous lire
    
    Reply ↓
bajb 6 juin 2020 at 15 h 46 min

Merci !Un grand merci.
Je suis toujours l’évolution d’une part mais une vision TRI est plus qu’intéressante !

Reply ↓
Arthur 7 novembre 2020 at 16 h 43 min

Bonjour,

Dans votre Exemple n°2 vous obtenez un TRI de 6,93% pourtant un bénéfice de 10€ sur 190€ d’apport représente un rendement réel de 10/190 = 5.26%.

J’utilisa la méthode de TRI pour calculer mon rendement, mais quand j’utilise un exemple simple comme celui de votre exemple 2, le TRI ne représente pas le rendement réel…

Reply ↓
- Jerome Leivrek Post author 7 novembre 2020 at 23 h 24 min
  
  Bonjour
  C’est parce que, ce que vous appelez le « rendement réel » n’est pas une bonne mesure du rendement. En effet, avec votre « rendement réel », vous faites comme si les 190 € avaient travaillé pendant 2 ans, alors que 100 € ont travaillé pendant un an, puis 190 € pendant une nouvelle année.
  JL
  
  Reply ↓

Le projet Lynch

Des stratégies simples pour investir et gagner en bourse